Math 430: Lecture 4a

Simple Linear Regression

Professor Catalina Medina

Why simple linear regression

Some of you may not have been exposed to it before and it is a good starting point for more complicated models.
It is very interpretable. If we can model out data with a model we can easily explain, why use a more complicated unexplainable model?

Example: Elephant Mass

Weighing elephants is not an easy task, but an elephant’s mass can help inform about appropriate diet and medicine for elephants in captivity.

Lalande et. al. 2022 figured height could be a useful proxy for elephants.

Example: Elephant Mass by height

The idea is to:

Collect height and mass for a sample of elephants.
Use that sample to fit a model, predicting mass from height.
Predict the mass for elephants outside of our sample using their height in the model, with some understanding of uncertainty.

1. Collect sample

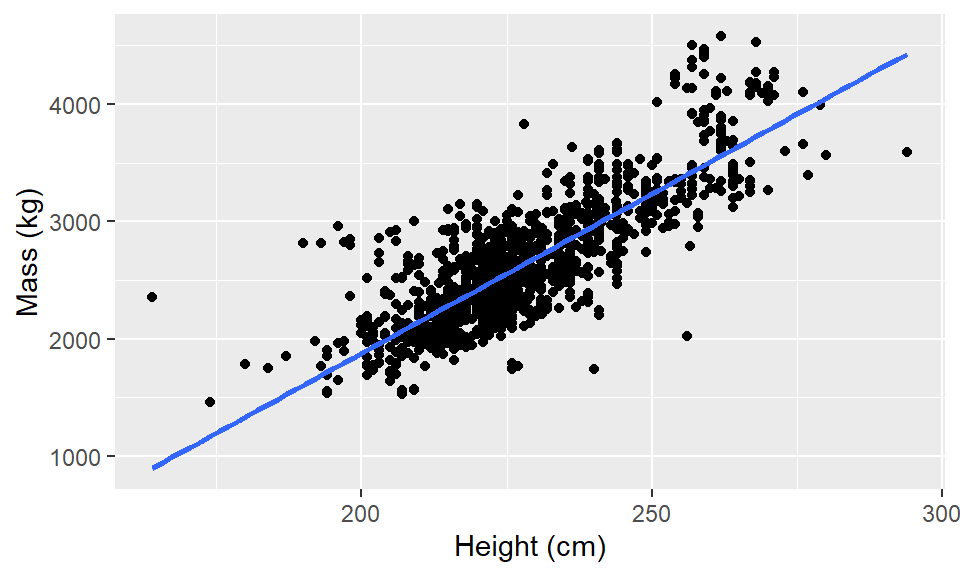
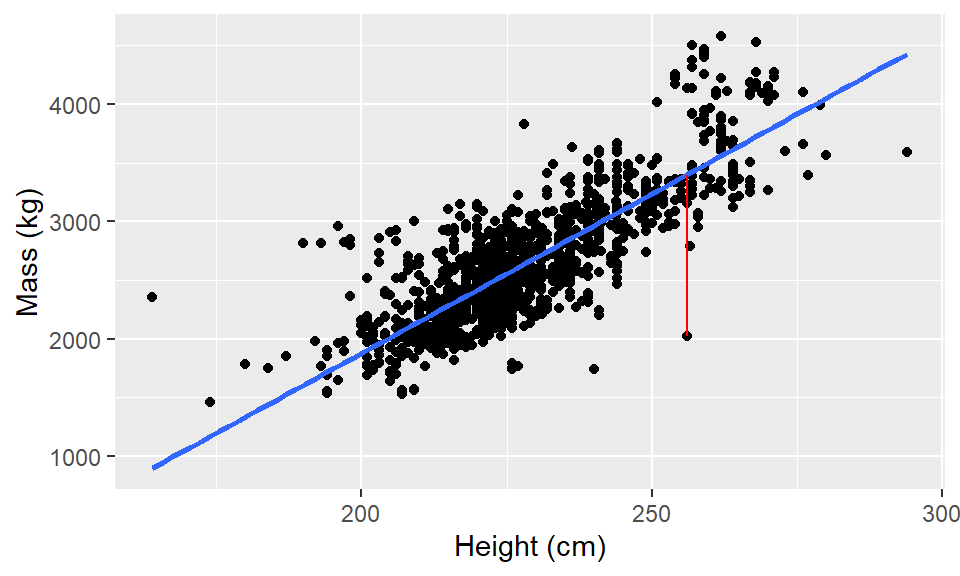
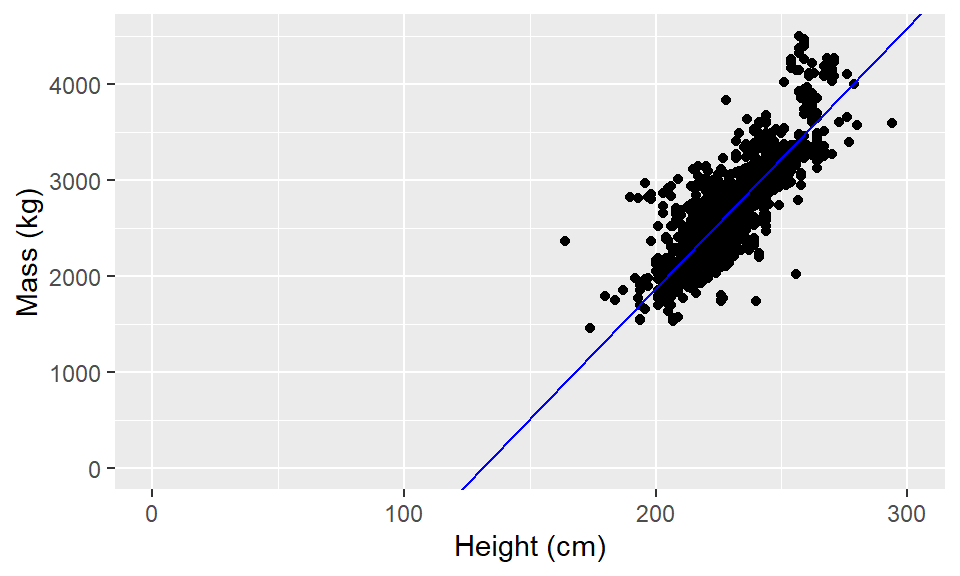
elephants <- read_csv(
  "http://csuci-math430.github.io/lectures/data/elephants.csv",
  show_col_types = FALSE
)

glimpse(elephants)

Rows: 1,470
Columns: 5
$ Sex    <chr> "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B"…
$ Age    <dbl> 58.96235, 59.03901, 59.12389, 59.29090, 59.37303, 59.45791, 59.…
$ Chest  <dbl> 359, 359, 359, 361, 360, 359, 361, 357, 360, 364, 355, 355, 325…
$ Height <dbl> 252, 252, 252, 253, 255, 254, 255, 256, 254, 255, 251, 257, 258…
$ Mass   <dbl> 3244, 3182, 3239, 3336, 3317, 3357, 3358, 3155, 3334, 3357, 324…

2. Fit model (visually)

ggplot(elephants, aes(x = Height, y = Mass)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  labs(x = "Height (cm)", y = "Mass (kg)")

Predict an elephant’s mass from its height

For a new elephant with an unknown mass, if its height is 250 meters

What would you predict its mass is?
If you were wagering money on your prediction, how much would you wager?

Simple linear regression

For numeric/quantitative response variables \(Y\), we can model a linear relationship between \(Y\) and an explanatory variable \(X\)

\[Y \approx \beta_0 + \beta_1 X\]

In our sample we know both \(X\) and \(Y\), but \(\beta_0\) and \(\beta_1\) are unknown parameters/coefficients.

\(\beta_0\) is the intercept
\(\beta_1\) is the slope

Fitting simple linear regression

Our mathematical theoretical model for individual \(i\) is

\[y_i = \beta_0 + \beta_1 x_i + \epsilon_i, \epsilon_i \overset{iid}{\sim} N(0, \sigma^2)\]

We will use our sample to get estimates for the parameters \(\beta_0\) & \(\beta_1\), to be able to predict \(y_i\)

\[\hat{y_i} = \hat{\beta_0} + \hat{\beta_1} x_i\]

How should we determine \(\hat{\beta_0}\) & \(\hat{\beta_1}\)?

Residuals

Let \(e_i = y_i −\hat{y}_i\) represents the ith residual

Minimizing the residual sum of squares

We will use the estimators that minimize the residual sum of squares, aka the least squares estimates

\[RSS(\beta_0, \beta_1) = \sum_{i = 1}^{n} e_i^2 = \sum_{i = 1}^{n}(y_i - \hat{y_i})^2\]

Why do you think we are choosing this as our function to optimize?

What could have been another option?

Minimizing the residual sum of squares

\[RSS(\beta_0, \beta_1) = \sum_{i = 1}^{n} e_i^2 = \sum_{i = 1}^{n}(y_i - \hat{y_i})^2.\]

How do we find the least squares estimates?

Take the derivative with respect to each variable.
Set each derivative equal to zero.
Solve for the estimators.

Least squares estimators

Proof in class.

Through some calculus we can show that the least squares estimators are

\[\hat{\beta}_1 = \frac{\sum_{i = 1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i = 1}^{n} (x_i - \bar{x})^2}\]

\[\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}\]

Do I expect you to be able to reproduce the proof?

No, but I do expect you to know the residual sum of squares formula and that \(\hat{\beta_0}\) and \(\hat{\beta_1}\) minimize it.

How do we compute \(\hat{\beta}_0\) and \(\hat{\beta}_1\) in practice?

elephant_model <- lm(Mass ~ Height, data = elephants)
summary(elephant_model)


Call:
lm(formula = Mass ~ Height, data = elephants)

Residuals:
     Min       1Q   Median       3Q      Max 
-1375.40  -193.73   -32.32   153.63  1457.10 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -3553.9303   111.5451  -31.86   <2e-16 ***
Height         27.1575     0.4885   55.59   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 305.3 on 1468 degrees of freedom
Multiple R-squared:  0.6779,    Adjusted R-squared:  0.6777 
F-statistic:  3090 on 1 and 1468 DF,  p-value: < 2.2e-16

Extracting our fitted model

elephant_model <- lm(Mass ~ Height, data = elephants)

Option 1: Tidyverse way

b0_hat <- broom::tidy(elephant_model) |> 
  filter(term == "(Intercept)") |> 
  pull(estimate)
b0_hat

[1] -3553.93

b1_hat <- broom::tidy(elephant_model) |> 
  filter(term == "Height") |> 
  pull(estimate)
b1_hat

[1] 27.15753

\(\hat{\beta}_0\) = -3553.9302816

\(\hat{\beta}_1\) = 27.1575293

Extracting our fitted model

elephant_model <- lm(Mass ~ Height, data = elephants)

Option 2: Base R way

b0_hat <- elephant_model$coefficients["(Intercept)"]
b0_hat

b1_hat <- elephant_model$coefficients["Height"]
b1_hat

\(\hat{\beta}_0\) = -3553.9302816

\(\hat{\beta}_1\) = 27.1575293

General predictive/fitted model:

\(\hat{y_i} = \hat{\beta}_0 +\hat{\beta}_1 x_i\)

Our predictive/fitted model:

\(\hat{Mass_i} =\) -3553.9302816 + 27.1575293 \(Height_i\)

Expectation of \(Y_i | X_i\)

Our mathematical theoretical model for individual \(i\) is

\[y_i = \beta_0 + \beta_1 x_i + \epsilon_i, \epsilon_i \overset{iid}{\sim} N(0, \sigma^2)\]

Therefore

\[\begin{equation*} \begin{split} &E[Y_i | X_i = x_i]\\ & = E[\beta_0 + \beta_1 X_i + \epsilon_i | X_i = x_i]\\ & = E[\beta_0 | X_i = x_i] + E[\beta_1 X_i | X_i = x_i] + E[\epsilon_i | X_i = x_i]\\ & = \beta_0 + \beta_1 x_i \end{split} \end{equation*}\]

Predicted / Expected mass

\(\hat{Mass_i} =\) -3553.9302816 + 27.1575293 \(Height_i\)

y_hat <- b0_hat + b1_hat * 250
y_hat

[1] 3235.452

For an elephant 250 meters tall we expect the mass to be 3235.45 kilograms.

We predict a 250 meter tall elephant to have a mass of 3235.45 kilograms, on average.

Interpreting y-intercept \(\beta_0\)

\[\beta_0 = E[Y_i | X_i = 0]\]

Proof: When \(X_i = 0\)

\[E[Y_i | X_i = 0] = E[\beta_0 +\beta_1 X_i + \epsilon_i | X_i = 0] = \beta_0.\]

\(\beta_0\) is the expected value of \(Y_i\) when \(X_i\) is zero.

For an elephant 0 meters tall we expect the mass to be -3553.93 kilograms.

The intercept does not always have practical meaning in context.

Interpreting slope \(\beta_1\)

\[\beta_1 = E[Y_i | X_i = x_i + 1] - E[Y_i | X_i = x_i]\]

Proof \[\begin{equation*} \begin{split} &E[Y_i | X_i = x_i + 1] - E[Y_i | X_i = x_i]\\ &=E[\beta_0 + \beta_1 X_i + \epsilon_i | X_i = x_i + 1]\\ &- E[\beta_0 + \beta_1 X_i + \epsilon_i | X_i = x_i] \\ &=\beta_0 + \beta_1 E[X_i | X_i = x_i + 1] - (\beta_0 + \beta_1 E[X_i | X_i = x_i]) \\ &= \beta_0 + \beta_1 (x_i + 1) - (\beta_0 + \beta_1 x_i)\\ &= \beta_0 + \beta_1 x_i + \beta_1 - \beta_0 - \beta_1 x_i\\ &= \beta_1 \end{split} \end{equation*}\]

Interpreting slope \(\beta_1\)

\[\beta_1 = E[Y_i | X_i = x_i + 1] - E[Y_i | X_i = x_i]\]

So \(\beta_1\) is the expected difference in the response for a 1 unit difference in \(X_i\).

For two elephant that differ in height by one meter we expect the difference in mass to be 27.16 kilograms.